TEMAS PRUEBA DE MATEMÁTICAS  MIERCOLES 21 DE AGOSTO

✅ Operaciones básicas con números naturales

Ver Video: Suma

Ver Video: Resta

Ver Video: Multiplicación

Ver Video: División

Ver Video: Problemas

✅ Potenciación y radicación de números naturales y sus propiedades

Ver Video: Potenciación 

Ver Video: Propiedades de la potenciación parte 1 

Ver Video: Propiedades de la potenciación parte 2 

Ver Video: Radicación

Ver Video: Propiedades de la radicación 

Ver Video: Problemas parte 1

Ver Video: Problemas parte 2

Ver Video: Problemas parte 3

✅ Múltiplos y divisores de un número

Ver Video: Múltiplos y divisores

Ver Video: Problemas

✅ Criterios de divisibilidad 

Ver Video: Criterios de divisibilidad Parte 1

Ver Video: Criterios de divisibilidad Parte 2

Ver Video: Criterios de divisibilidad Parte 3

✅ Mínimo común múltiplo (MCM) y máximo común denominador (MCD)

Ver Video: Tema MCM

Ver Video: Tema MCD

Ver video: Problemas

TEMAS PRUEBA DE ESTADÍSTICA  MIERCOLES 21 DE AGOSTO

✅ Tablas de frecuencias

Ver Video: Tab. de Frec.

✅ Gráficos estadísticos 

Ver Video: Graf. Estad. 

✅ Medidas de tendencia central (media, moda y mediana)

Ver Video: MTC

TEMAS PRUEBA DE GEOMETRÍA  MIERCOLES 21 DE AGOSTO

✅ Polígonos: definición, elementos y su clasificación.

Ver Video: Generalidades de los polígonos parte 1

Ver Video: Generalidades de los polígonos parte 2

✅ Ángulos internos de un polígono y polígonos congruentes.

Ver Video: Ángulos internos

Ver Video: Polígonos congruentes

✅ Perímetro de un polígono.

Ver Video: Perímetro de figuras

✅ Plano cartesiano.

Ver Video: Ubicación de puntos 

MATEMÁTICAS

Tema: MÍNIMO COMÚN MÚLTIPLO Y MÁXIMO COMÚN DIVISOR

Mínimo Común Múltiplo (MCM)

Definición:

El Mínimo Común Múltiplo (MCM) de dos o más números es el número más pequeño que es múltiplo de todos esos números. Es decir, es el múltiplo más bajo que comparten dos o más números.

Ejemplo 1:

Encuentra el MCM de 4 y 6.

Los múltiplos de 4 son: M4 = {4, 8, 12, 16, 20, 24, ...}

Los múltiplos de 6 son: M6 = {6, 12, 18, 24, ...}

Los múltiplos que tienen en común el 4 y el 6 son el 12 y el 24, siendo el 12 el menor de los múltiplos, o en otras palabras, es el primer número que aparece en ambas listas de múltiplos . Por lo tanto, el MCM del 4 y el 6 es el 12. Esto se escribe o representa así MCM (4, 6) = 12

Ejemplo 2:

Encuentra el MCM de 3, 5 y 15.

Los múltiplos de 3 son: M3 = { 3, 6, 9, 12, 15, 18, ... }

Los múltiplos de 5 son: M5 = {5, 10, 15, 20, 25, ... }

Los múltiplos de 15 son: M15 = {15, 30, 45, ... }

Los múltiplos que tienen en común el 3, 5 y 15 es 15 porque es el número más pequeño que aparece en todas las listas. Entonces, MCM (3, 5, 15) = 15 

Máximo Común Divisor (MCD)

Definición:

El Máximo Común Divisor (MCD) de dos o más números es el número más grande que divide exactamente a todos esos números, es decir, el divisor común más grande.

Ejemplo 1:

Encuentra el MCD de 8 y 12.

Los divisores de 8 son: D8 = {1, 2, 4, 8}

Los divisores de 12 son: D12 = {1, 2, 3, 4, 6, 12}

Los divisores que tienen en común el 8 y 12 son el 1, 2 y 4, siendo este último número el divisor común más grande entre ambos. Por lo tanto, el MCD del 8 y el 12 es el 4. Esto se escribe o representa así MCD (8, 12) = 4

Ejemplo 2:

Encuentra el MCD de 18 y 24.

Los divisores de 18 son: D18 = {1, 2, 3, 6, 9, 18}

Los divisores de 24 son: D24 = {1, 2, 3, 4, 6, 8, 12, 24}

Por lo tanto, El MCD de 18 y 24 es 6. Es decir, MCD (18, 24) = 6

Casos en los que debo aplicar m.c.m. o m.c.d. para resolver problemas.

Problemas que se resuelven a través de m.c.m.

• Coincidencia: Cuando dos o más eventos coinciden al mismo tiempo.
• Ciclo repetitivo: Situaciones que se repiten cada cierto intervalo.
• Frecuencia común: Encontrar cuándo algo ocurre al mismo tiempo o con la misma frecuencia.
• Menor intervalo común: El tiempo o la cantidad más pequeña que permite que dos o más eventos ocurran simultáneamente.
• Sincronizar: Hacer que dos o más eventos sucedan al mismo tiempo.
• Múltiplos o repeticiones: Referente a eventos o cantidades que se repiten.

Problemas que se resuelven a través de m.c.d.

• Distribuir equitativamente: Repartir algo en partes iguales entre grupos.
• Mayor cantidad posible: Encontrar la mayor cantidad que permite una distribución igual.
• Divisiones exactas: Cuando se quiere dividir algo (tiempo, espacio, objetos) en partes iguales sin que sobre nada.
• Agrupar: Formar grupos con la misma cantidad de elementos.
• Reducir a partes más pequeñas: Encontrar el número más grande que divide uniformemente a todos los elementos.
• Simplificar: En contextos de simplificación de fracciones, o al reducir algo a su mínima expresión.

Problemas Relacionados con MCM y MCD

Problema 1:

Tres amigos deciden que se encontrarán cada 4, 6 y 8 días respectivamente. Si se encuentran hoy, ¿cuántos días pasarán antes de que se encuentren todos juntos nuevamente?

Solución:

Esto es un problema de MCM. Debemos encontrar el MCM de 4, 6 y 8.

Múltiplos de 4: 4, 8, 12, 16, 20, 24, ...

Múltiplos de 6: 6, 12, 18, 24, ...

Múltiplos de 8: 8, 16, 24, ...

El MCM es 24, por lo que se encontrarán nuevamente en 24 días.

Problema 2:

Dos relojes suenan a la vez. Uno suena cada 9 horas y el otro cada 12 horas. ¿Cuántas horas pasarán hasta que vuelvan a sonar juntos?

Solución:

Esto también es un problema de MCM. Debemos encontrar el MCM de 9 y 12.

Múltiplos de 9: 9, 18, 27, 36, ...

Múltiplos de 12: 12, 24, 36, ...

El MCM es 36, por lo que pasarán 36 horas hasta que suenen juntos de nuevo.

Problema 3:

Un granjero tiene 18, 24 y 30 árboles y quiere organizar los árboles en filas con la misma cantidad de árboles en cada fila. ¿Cuál es la cantidad máxima de árboles que puede tener cada fila?

Solución:

Este es un problema de MCD. Debemos encontrar el MCD de 18, 24 y 30.

Divisores de 18: 1, 2, 3, 6, 9, 18.

Divisores de 24: 1, 2, 3, 4, 6, 8, 12, 24.

Divisores de 30: 1, 2, 3, 5, 6, 10, 15, 30.

El MCD es 6, por lo que el granjero puede organizar los árboles en filas de 6.

MATEMÁTICAS

Tema: NÚMEROS PRIMOS Y NÚMEROS COMPUESTOS 

Los números primos y los números compuestos son dos tipos de números enteros que se diferencian por la cantidad de divisores que poseen.

Números Primos: Un número primo es un número entero mayor que 1 que solo tiene dos divisores: 1 y él mismo. En otras palabras, un número primo no puede ser dividido exactamente por ningún otro número entero positivo aparte de 1 y de sí mismo. 

Algunos ejemplos de números primos son 2, 3, 5, 7, 11, 13, y así sucesivamente.

Números Compuestos: Un número compuesto es un número entero mayor que 1 que tiene más de dos divisores. Esto significa que un número compuesto puede ser dividido exactamente por al menos un número entero positivo además de 1 y de sí mismo. 

Ejemplos de números compuestos son 4, 6, 8, 9, 12, 15, entre otros. 

Ejemplos

1. El número 7

   • D7 ={1, 7}.
   • Explicación: El número 7 solo puede ser dividido exactamente por 1 y por 7. No tiene otros divisores. Por lo tanto, 7 es un número primo.

2. El número 9

   • D9 ={1, 3, 9}.
   • Explicación: El número 9 puede ser dividido exactamente por 1, por 3 y por 9. Como tiene más de dos divisores, 9 es un número compuesto.

3. El número 11

• D11 ={1, 11}.
• Explicación: El número 11 solo puede ser dividido exactamente por 1 y por 11. No tiene otros divisores, por lo que 11 es un número primo.

Descomposición de un número en factores primos

La descomposición en factores primos es el proceso de expresar un número entero como un producto de números primos. Es importante recordar que un número primo es un número que solo tiene dos divisores: 1 y él mismo. El objetivo de la descomposición en factores primos es descomponer un número compuesto (un número que tiene más de dos divisores) en un producto de números primos. Este proceso es útil en varios contextos matemáticos, como en la simplificación de fracciones, la resolución de problemas de divisibilidad y el cálculo del mínimo común múltiplo (MCM) o el máximo común divisor (MCD).

Ejemplos

1. Descomposición del número 60

   • Comenzamos dividiendo el número 60 por el menor número primo, que es 2:
     $$60 \div 2 = 30$$
     
   • Luego, dividimos 30 por 2 nuevamente: $$30 \div 2 = 15$$
     
   • El número 15 no es divisible por 2, por lo que pasamos al siguiente número primo, que es 3:
     $$15 \div 3 = 5$$
     
   • Finalmente, 5 es un número primo, así que terminamos el proceso. La descomposición en factores primos de 60 es:
     $$60 = 2^2 \times 3 \times 5$$
     

2. Descomposición del número 84

   • Dividimos 84 por 2: $$84 \div 2 = 42$$
     
   • Dividimos 42 por 2 nuevamente: $$42 \div 2 = 21$$
     
   • El número 21 no es divisible por 2, así que usamos el siguiente número primo, 3:
     $$21 \div 3 = 7$$
     
   • Como 7 es un número primo, hemos terminado. La descomposición en factores primos de 84 es:
     $$84 = 2^2 \times 3 \times 7$$
     

3. Descomposición del número 100

   • Dividimos 100 por 2: $$100 \div 2 = 50$$
     
   • Dividimos 50 por 2 nuevamente: $$50 \div 2 = 25$$
     
   • El número 25 no es divisible por 2, por lo que pasamos al siguiente número primo, 3, que tampoco es divisor de 25. Pasamos entonces al siguiente número primo, 5:
     $$25 \div 5 = 5$$
     
   • Como 5 es un número primo, terminamos el proceso. La descomposición en factores primos de 100 es:
     $$100 = 2^2 \times 5^2$$

Una forma común, sencilla y organizada para descomponer un número en factores primos es el método vertical. A continuación, se describen los pasos para utilizar este método:

Pasos del Método Vertical

1. Escribe el número a descomponer:

   • Coloca el número en la parte superior y a la izquierda de una línea vertical o barra vertical. A la derecha de la barra, colocarás los factores primos que vayas obteniendo.

2. Divide el número por el menor número primo posible:

   • Comienza dividiendo el número por el menor número primo, que es 2. Si el número es divisible entre 2 (es decir, si es par), escribe 2 a la derecha de la barra y el cociente debajo del número original. Si el número no es divisible por 2, entonces, busca el siguiente número primo (3, 5, 7...) que divida al número original. 

3. Continúa dividiendo el cociente por números primos:

   • Toma el cociente obtenido y vuelve a dividirlo por el menor número primo posible (puede ser nuevamente 2, o 3 si ya no es divisible entre 2, y así sucesivamente). Escribe el nuevo cociente debajo del anterior y el número primo divisor a la derecha de la barra.

4. Repite el proceso hasta llegar a 1:

   • Sigue dividiendo el último cociente por números primos hasta que obtengas 1 como cociente. Cada número primo divisor que utilices se anota a la derecha de la barra.

5. Multiplica los números primos obtenidos:

• Los números primos que has anotado a la derecha de la barra son los factores primos del número original. El número original es el producto de estos factores primos.

A continuación, se muestran las descomposiciones en factores primos de los números 60, 84 y 100 usando el método vertical.

MATEMÁTICAS

Tema: CRITERIOS DE DIVISIBILIDAD

Los criterios de divisibilidad permiten determinar si un número es divisible por otro sin realizar la división completa. Aquí te presento los criterios de divisibilidad más importantes, hasta el 25, con tres ejemplos para cada uno:

1. Divisibilidad por 2:

• Criterio: Un número es divisible por 2 si termina en 0, 2, 4, 6 u 8. es decir, termina en un número par.
• Ejemplos:
  1. 48: Termina en 8 (es divisible por 2).
  2. 122: Termina en 2 (es divisible por 2).
  3. 37: Termina en 7 (no es divisible por 2).

2. Divisibilidad por 3:

• Criterio: Un número es divisible por 3 si la suma de sus dígitos es un múltiplo del 3.
• Ejemplos:
  1. 81: 8 + 1 = 9 (9 es divisible por 3).
  2. 123: 1 + 2 + 3 = 6 (6 es divisible por 3).
  3. 56: 5 + 6 = 11 (11 no es divisible por 3).

3. Divisibilidad por 4:

• Criterio: Un número es divisible por 4 si los dos últimos dígitos forman un número divisible por 4 o termina en 00.
• Ejemplos:
  1. 124: Los últimos dos dígitos son 24 (24 es divisible por 4).
  2. 200: Los últimos dos dígitos son 00 (00 es divisible por 4).
  3. 43: Los últimos dos dígitos son 43 (43 no es divisible por 4).

4. Divisibilidad por 5:

• Criterio: Un número es divisible por 5 si termina en 0 o 5.
• Ejemplos:
  1. 75: Termina en 5 (es divisible por 5).
  2. 90: Termina en 0 (es divisible por 5).
  3. 86: Termina en 6 (no es divisible por 5).

5. Divisibilidad por 6:

• Criterio: Un número es divisible por 6 si es divisible por 2 y por 3.
• Ejemplos:
  1. 72: Es divisible por 2 (termina en 2) y por 3 (7 + 2 = 9, divisible por 3).
  2. 54: Es divisible por 2 (termina en 4) y por 3 (5 + 4 = 9, divisible por 3).
  3. 40: Es divisible por 2 pero no por 3 (4 + 0 = 4, no divisible por 3), por lo tanto no es divisible por 6.

6. Divisibilidad por 7:

• Criterio: Un número es divisible por 7 si la diferencia entre el resto del número al quitar la última cifra y doble del último dígito, da como resultado un número múltiplo del 7
• Ejemplos:
  1. 154: 15 - (2 × 4) = 15 - 8 = 7 (7 es divisible por 7).
  2. 203: 20 - (2 × 3) = 20 - 6 = 14 (14 es divisible por 7).
  3. 50: 5 - (2 × 0) = 5 (5 no es divisible por 7).

7. Divisibilidad por 9:

• Criterio: Un número es divisible por 9 si la suma de sus dígitos es múltiplo del 9.
• Ejemplos:
  1. 729: 7 + 2 + 9 = 18 (18 es divisible por 9).
  2. 81: 8 + 1 = 9 (9 es divisible por 9).
  3. 45: 4 + 5 = 9 (9 es divisible por 9).

8. Divisibilidad por 10:

• Criterio: Un número es divisible por 10 si termina en 0.
• Ejemplos:
  1. 70: Termina en 0 (es divisible por 10).
  2. 150: Termina en 0 (es divisible por 10).
  3. 42: Termina en 2 (no es divisible por 10).

9. Divisibilidad por 11:

• Criterio: Un número es divisible por 11 si la diferencia entre la suma de sus dígitos en posiciones impares y la suma de sus dígitos en posiciones pares es múltiplo de 11 o 0.
• Ejemplos:
  1. 121: (1 + 1) - 2 = 0 (es divisible por 11).
  2. 242: (2 + 2) - 4 = 0 (es divisible por 11).
  3. 123: (1 + 3) - 2 = 2 (no es divisible por 11).

ESTADÍSTICA

Tema: REPRESENTACIÓN DE DATOS CON GRÁFICOS ESTADÍSTICOS

Los gráficos estadísticos son herramientas visuales que permiten representar datos de manera clara y concisa. Aquí te dejo algunos de los gráficos estadísticos más importantes y comunes:

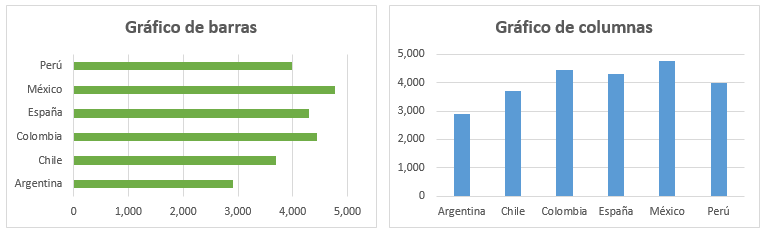
1. Gráfico de Barras:

• Uso: Comparar cantidades entre diferentes categorías.
• Descripción: Las categorías se representan en el eje horizontal (eje X) y las cantidades en el eje vertical (eje Y) mediante barras.
• Ejemplo. La imagen de la izquierda corresponde a un gráfico de barras horizontal, mientras que la imagen de la derecha muestra un gráfico de barras vertical o de columnas. 

2. Histograma:

• Uso: Mostrar la distribución de un conjunto de datos continuos.
• Descripción: Similar al gráfico de barras, pero con datos agrupados en intervalos (bins), mostrando la frecuencia de los datos dentro de cada intervalo.
• Ejemplo.

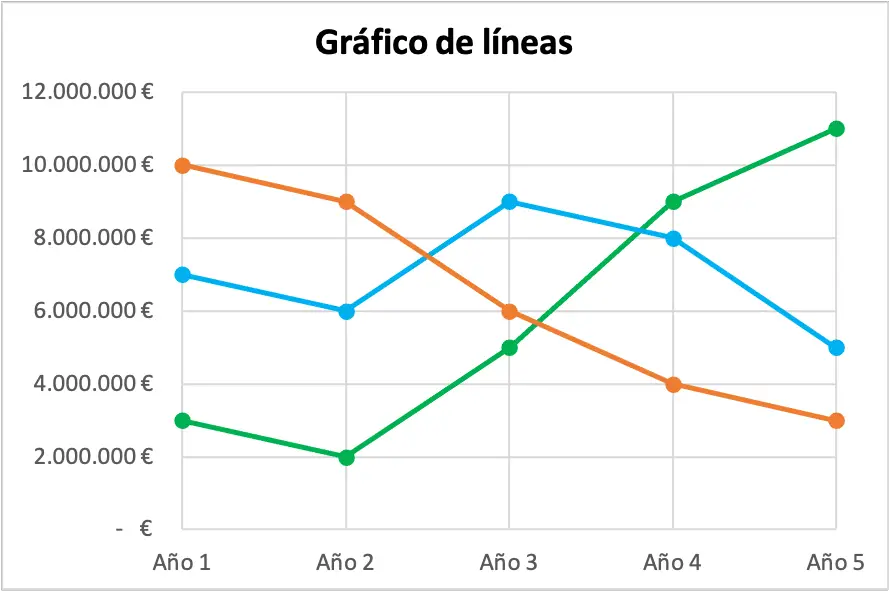
3. Gráfico de Líneas:

• Uso: Mostrar tendencias a lo largo del tiempo.
• Descripción: Los puntos de datos están conectados por líneas, y es común en análisis de series temporales.
• Ejemplo.

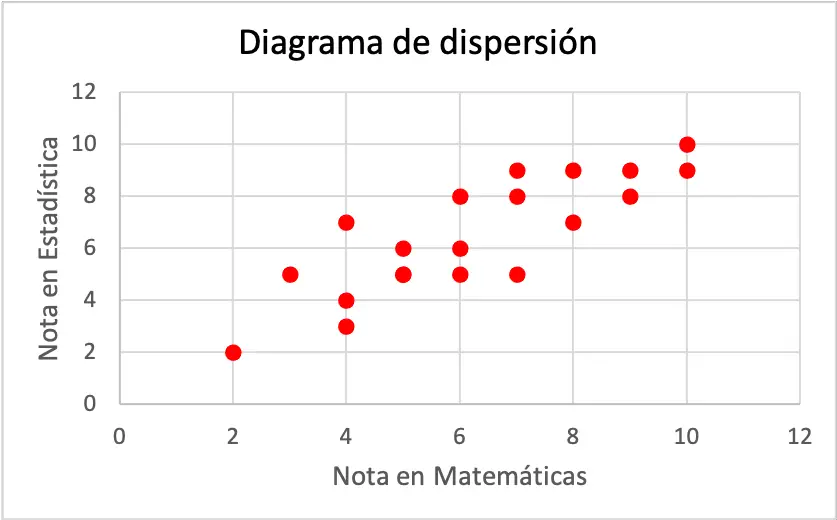
4. Diagrama de Dispersión:

• Uso: Mostrar la relación entre dos variables numéricas.
• Descripción: Cada punto en el gráfico representa un par de valores (X, Y). Es útil para identificar correlaciones o patrones.
• Ejemplo. 

5. Gráfico Circular (Pastel o Pie Chart):

• Uso: Representar proporciones relativas de un conjunto de datos categóricos.
• Descripción: El gráfico se divide en secciones o "rebanadas" que representan la proporción de cada categoría.
• Ejemplo.